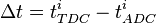Difference between revisions of "First look at TOF calibration"

From GlueXWiki
Jump to: navigation, search
 
(30 intermediate revisions by the same user not shown)
Line 5: Line 5:
 
*# take care of the 6fold trigger timing shift in the TDC (24ns window)
 
*# take care of the 6fold trigger timing shift in the TDC (24ns window)
  
−
* do a rough determination of the walk correction by using the time in the ADC as reference.
+
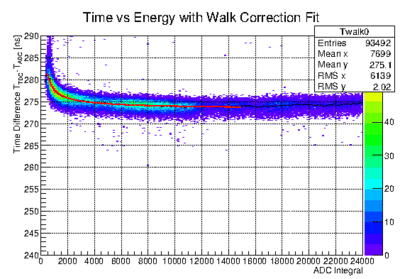
* Do a rough determination of the walk correction by using the time in the ADC as reference.
 
*# calculate Time difference: <math>\Delta t = t^{i}_{TDC}-t^{i}_{ADC}</math>  
 
*# calculate Time difference: <math>\Delta t = t^{i}_{TDC}-t^{i}_{ADC}</math>  
 
*# calculate Integral: I = pulse_integral - pulse_pedestal*nsamples
 
*# calculate Integral: I = pulse_integral - pulse_pedestal*nsamples
−
*# [[File:walkcorr.gif|200px|||example of walk correction fit]]
+
*# [[File:w.gif|400px|tumb||walk correction fit]]
 +
*# Note: the minimum ionizing peak is between 6000 and 10000
 +
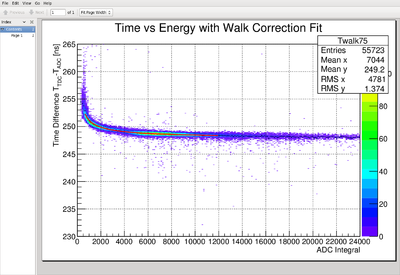
*# After using the correct timing conversion of 23.4375 ps/bin the following much narrower distribution is achieved
 +
*# [[File:Screenshot-walk_correction_example.pdf.png|400px|tumb||walk correction and fit]]  
 +
 
 +
* Do mean time comparison between different planes
 +
*# calculate MeanTime of Paddle i in plane j: <math> MT^{i}_{plane j} = (t_{right} + t_{left})/2. </math>
 +
*# calculate MeanTime for all Paddles n in plane k: <math> MT^{n}_{plane k} = (t_{right} + t_{left})/2. </math>
 +
*# For each Reference paddle in plane j: <math> MT^{paddle_{n}}_{plane_{k}} - MT^{REF}_{plane_{j}} </math>
 +
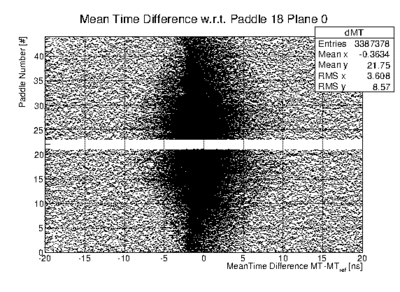
*# [[File:example_mtdiff.gif|400px]]
 +
*# and after using the correct timing conversion of 23.4375ps/bin:
 +
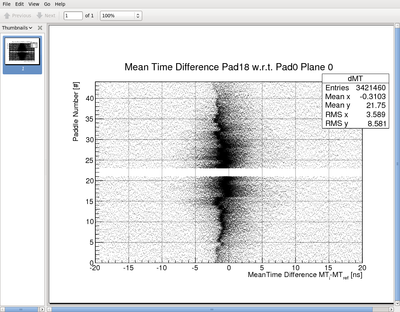
*# [[File:mantimediff_goodtiming.png|400px]]
 +
*# Fit the meant time peak of each projection. This is the relative mean-time difference.
 +
*# [[File:Fit_projection_example1.gif|400px]] example 1
 +
*# [[File:Fit_projection_example2.gif|400px]] example 2
 +
*# and now a good example after using the correct timing conversion
 +
*# [[File:Screenshot-mtdiff_vs_padnum_proj_example42.pdf.png|400px]]
 +
*# and an example where the automatic fit failed because the meantime peak is smaller than the background
 +
*# [[File:Screenshot-mtdiff_vs_padnum_proj_example44.pdf.png|400px]]
 +
*# Do this for each paddle in the first plane as reference paddle.
 +
*# Choose one paddle in the first plane as THE REFERENCE PADDLE
 +
*# Calculate the difference between the fit results of each paddle in the first plane w.r.t. THE REFERENCE PADDLE and fit the distribution
 +
*# [[File:Meantime_average_to_refpaddle_example.gif|400px]] average difference of mean time to REFERENCE PADDLE
 +
*# Now we have offsets for the Mean-Time for all Paddles w.r.t. THE REFERENCE PADDLE
 +
 
 +
* Do time difference comparison of one paddle with the paddle number in the other plane
 +
*# calculate time difference: <math> \Delta t^{i}_{plane j} = (t_{right} - t_{left})/2. </math>
 +
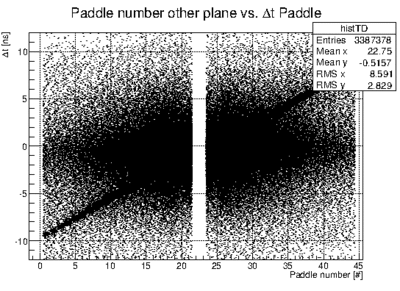
*# plot this time difference vs. paddle number of paddles that got hit in the other plane
 +
*# [[File:PaddleNumber_vs_deltat_example.gif|400px]]
 +
*# again look at each projection and fit the <math>\Delta t</math> peak
 +
*# [[File:deltat_fitposition_example.gif|400px]]  [[File:deltat_fitposition_p18_example.gif|400px]]  example fits
 +
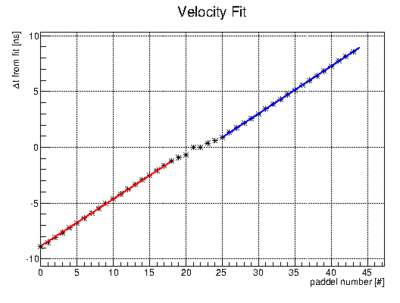
*# now one can also plot the fit results as a function of paddle number. The inverse slope is the speed module paddle pitch
 +
*# [[File:velocity_example.gif|400px]]
 +
*# one can also plot the difference between symmetric paddles around the beam hole <math>\Delta t_{left} - \Delta t_{right}</math>
 +
*# [[File:timediff_planesymmetry_example.gif|400px]] choose the intersection at zero for the time difference offset
 +
 
 +
* Now we have offsets for time difference (TD) and mean time (MT)
 +
*# offset for the left pmt: <math> c_{left} = (MT-TD)/2.  </math>
 +
*# offset for the right pmt: <math> c_{right} = (MT+TD)/2.  </math>
 +
*# as a bonus we get the effective speed of light for each paddle.

Latest revision as of 13:32, 17 April 2015

First Look

  • first select data sample with the following conditions:
    1. only consider hits within 50ns of the timing peak both for ADC data and TDC data
    2. only consider paddles that have hits on both ends
    3. take care of the 6fold trigger timing shift in the TDC (24ns window)
  • Do a rough determination of the walk correction by using the time in the ADC as reference.
    1. calculate Time difference: \Delta t=t_{{TDC}}^{{i}}-t_{{ADC}}^{{i}}
    2. calculate Integral: I = pulse_integral - pulse_pedestal*nsamples
    3. walk correction fit
    4. Note: the minimum ionizing peak is between 6000 and 10000
    5. After using the correct timing conversion of 23.4375 ps/bin the following much narrower distribution is achieved
    6. walk correction and fit
  • Do mean time comparison between different planes
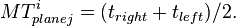
    1. calculate MeanTime of Paddle i in plane j: MT_{{planej}}^{{i}}=(t_{{right}}+t_{{left}})/2.
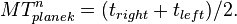
    2. calculate MeanTime for all Paddles n in plane k: MT_{{planek}}^{{n}}=(t_{{right}}+t_{{left}})/2.
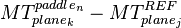
    3. For each Reference paddle in plane j: MT_{{plane_{{k}}}}^{{paddle_{{n}}}}-MT_{{plane_{{j}}}}^{{REF}}
    4. Example mtdiff.gif
    5. and after using the correct timing conversion of 23.4375ps/bin:
    6. Mantimediff goodtiming.png
    7. Fit the meant time peak of each projection. This is the relative mean-time difference.
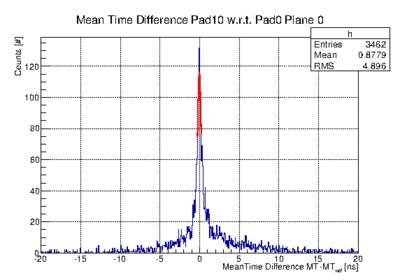    8. Fit projection example1.gif example 1
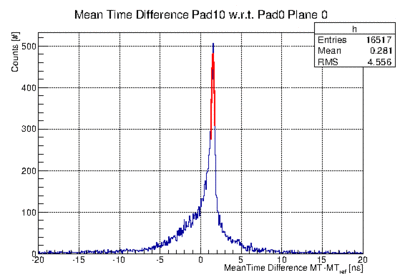    9. Fit projection example2.gif example 2
    10. and now a good example after using the correct timing conversion
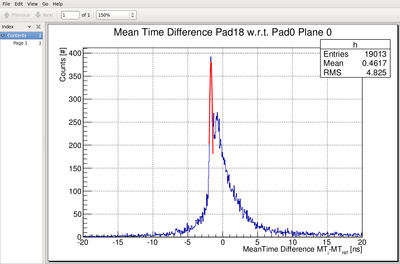
    11. Screenshot-mtdiff vs padnum proj example42.pdf.png
    12. and an example where the automatic fit failed because the meantime peak is smaller than the background
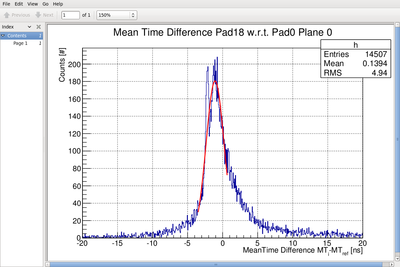
    13. Screenshot-mtdiff vs padnum proj example44.pdf.png
    14. Do this for each paddle in the first plane as reference paddle.
    15. Choose one paddle in the first plane as THE REFERENCE PADDLE
    16. Calculate the difference between the fit results of each paddle in the first plane w.r.t. THE REFERENCE PADDLE and fit the distribution
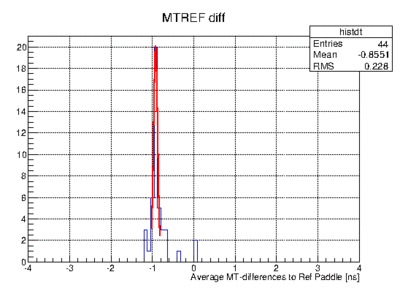    17. Meantime average to refpaddle example.gif average difference of mean time to REFERENCE PADDLE
    18. Now we have offsets for the Mean-Time for all Paddles w.r.t. THE REFERENCE PADDLE
  • Do time difference comparison of one paddle with the paddle number in the other plane
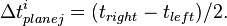
    1. calculate time difference: \Delta t_{{planej}}^{{i}}=(t_{{right}}-t_{{left}})/2.
    2. plot this time difference vs. paddle number of paddles that got hit in the other plane
    3. PaddleNumber vs deltat example.gif
    4. again look at each projection and fit the 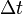\Delta t peak
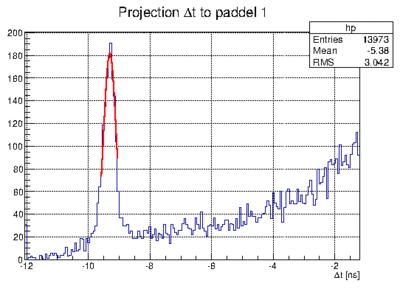
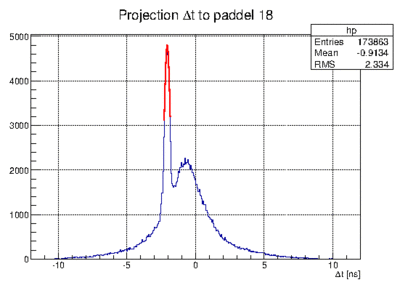    5. Deltat fitposition example.gif Deltat fitposition p18 example.gif example fits
    6. now one can also plot the fit results as a function of paddle number. The inverse slope is the speed module paddle pitch
    7. Velocity example.gif
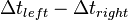
    8. one can also plot the difference between symmetric paddles around the beam hole \Delta t_{{left}}-\Delta t_{{right}}
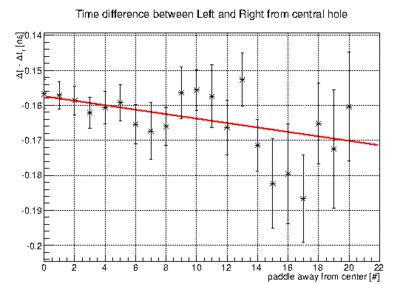    9. Timediff planesymmetry example.gif choose the intersection at zero for the time difference offset
  • Now we have offsets for time difference (TD) and mean time (MT)
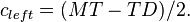
    1. offset for the left pmt: c_{{left}}=(MT-TD)/2.
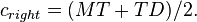
    2. offset for the right pmt: c_{{right}}=(MT+TD)/2.
    3. as a bonus we get the effective speed of light for each paddle.
Retrieved from "https://halldweb.jlab.org/wiki/index.php?title=First_look_at_TOF_calibration&oldid=66263"