Difference between revisions of "Gain Adjustments"
From GlueXWiki
(→Table of Gains) |
|||
| Line 19: | Line 19: | ||
{| class="wikitable" style="text-align: left; width: 700px; height: 900px; | {| class="wikitable" style="text-align: left; width: 700px; height: 900px; | ||
|- | |- | ||
| + | ! position | ||
! base ID | ! base ID | ||
! V<sub>0</sub> | ! V<sub>0</sub> | ||
! V<sub>0</sub>+100 | ! V<sub>0</sub>+100 | ||
|- | |- | ||
| − | | | + | | H1 |
| − | | | + | | 0x732c79 |
| − | | | + | | 1421.96 |
| + | | 1521.96 | ||
|- | |- | ||
| + | | H2 | ||
| 0x72c932 | | 0x72c932 | ||
| 1413.45 | | 1413.45 | ||
| 1513.45 | | 1513.45 | ||
|- | |- | ||
| + | | H3 | ||
| + | | 0x72360e | ||
| + | | 1446.51 | ||
| + | | 1546.51 | ||
| + | |- | ||
| + | | H4 | ||
| + | | 0x738545 | ||
| + | | 1493.05 | ||
| + | | 1593.05 | ||
| + | |- | ||
| + | | H5 | ||
| 0x733d10 | | 0x733d10 | ||
| 1483.08 | | 1483.08 | ||
| 1583.08 | | 1583.08 | ||
|- | |- | ||
| − | | | + | | V1 |
| − | | | + | | 0x733e06 |
| − | + | | 1451.23 | |
| − | + | | 1551.23 | |
| − | + | ||
| − | | | + | |
| − | | | + | |
|- | |- | ||
| + | | V2 | ||
| 0x72dacc | | 0x72dacc | ||
| 1477.14 | | 1477.14 | ||
| 1577.14 | | 1577.14 | ||
|- | |- | ||
| − | | | + | | V3 |
| − | + | ||
| − | + | ||
| − | + | ||
| 0x72bb3f | | 0x72bb3f | ||
| 1365.49 | | 1365.49 | ||
| 1465.49 | | 1465.49 | ||
|- | |- | ||
| − | | | + | | V4 |
| − | | | + | | 0x72579b |
| − | | | + | | 1442.73 |
| + | | 1542.73 | ||
|- | |- | ||
| − | | | + | | V5 |
| − | | | + | | 0x738516 |
| − | | | + | | 1436.49 |
| + | | 1536.49 | ||
|- | |- | ||
| remote | | remote | ||
| + | | | ||
| 1489.09 | | 1489.09 | ||
| 1589.09 | | 1589.09 | ||
|} | |} | ||
Revision as of 11:55, 4 November 2011
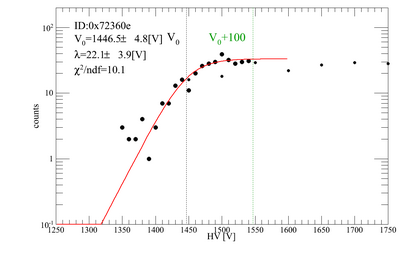
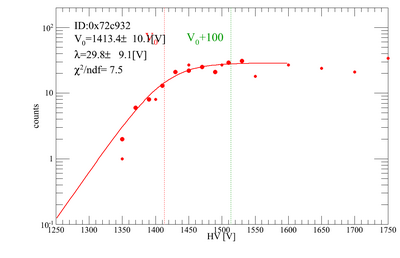
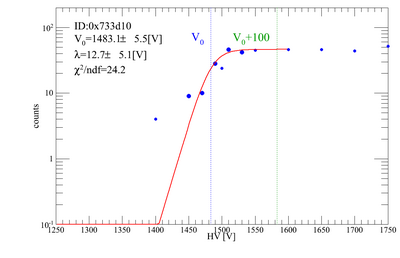
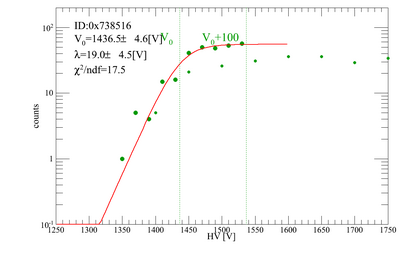
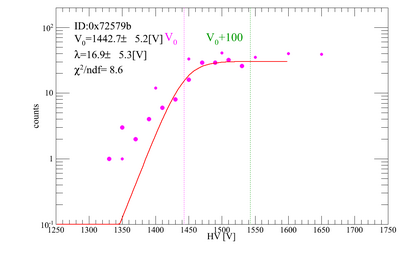
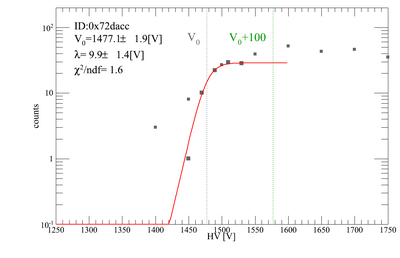
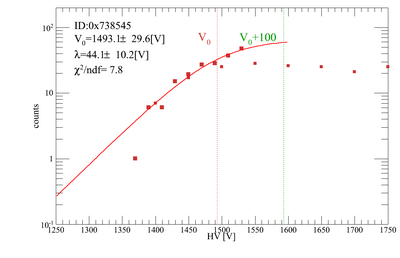
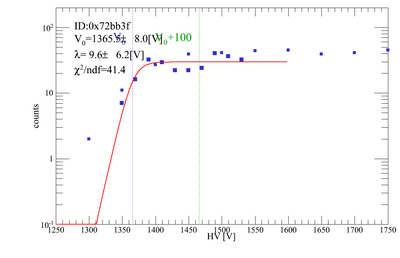
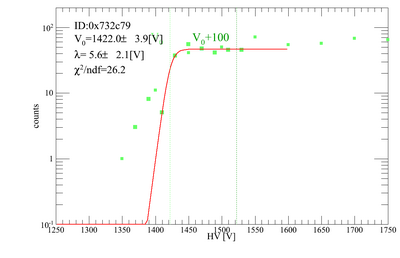
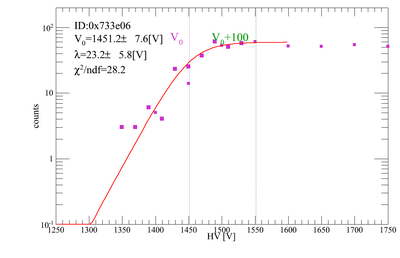
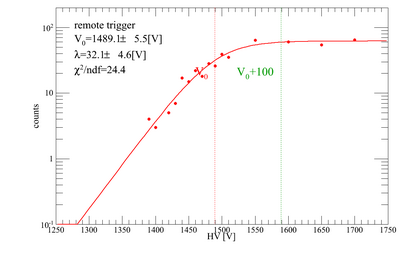
Gains for each PMT/base combination to be used for the beamtest have been tested. Our method was to place two triggers on top of each other, and count the coincidence rate of cosmic rays as we vary the HV on the trigger we want to test. The other trigger was kept at 1700 V. Below are plots for the gain adjustments. There are 10 trigger scintillators, and 1 remote trigger.
The gains were fit with a "turnon function", the same we use for the PMT tests, and the central value of the turnon curve (V0) was obtained. The nominal HV values for each PMT/base combination is V0+100 [V].
Figure of Gains
- Triggers:
- Remote Trigger:
Table of Gains
| position | base ID | V0 | V0+100 |
|---|---|---|---|
| H1 | 0x732c79 | 1421.96 | 1521.96 |
| H2 | 0x72c932 | 1413.45 | 1513.45 |
| H3 | 0x72360e | 1446.51 | 1546.51 |
| H4 | 0x738545 | 1493.05 | 1593.05 |
| H5 | 0x733d10 | 1483.08 | 1583.08 |
| V1 | 0x733e06 | 1451.23 | 1551.23 |
| V2 | 0x72dacc | 1477.14 | 1577.14 |
| V3 | 0x72bb3f | 1365.49 | 1465.49 |
| V4 | 0x72579b | 1442.73 | 1542.73 |
| V5 | 0x738516 | 1436.49 | 1536.49 |
| remote | 1489.09 | 1589.09 |