GlueX Physics Quark Model
Contents
GlueX Physics
Review Papers
Mesons in the Quark Model
Conserved Quantities in the Strong Interaction
To do this, I want to start with the very basics of the strong interaction, namely the conserved quantities, J, P, C, ···. With this, I want to look at spectroscopy within one specific model, the constituent quark model. This model is by no means perfect. It provides no explanation for confinement, and the role of gluons is not obvious. It also makes no absolute mass predictions, and no absolute rate predictions for decays. However it does make a rather large number of very good predictions. It also provides a very natural framework within which to classify mesons. It provides a natural handle to address issues such as structure and decays, and even makes some rather nice predictions for relative decay rates.
The strong interaction conserves a number of quantities, some of which are listed here.
B Baryon number.
Q Electric charge.
J Angular momentum.
S Strangeness.
I Strong isospin.
P Parity.
C Charge conjugation.
G G–parity.
Those that are used will be explained as we go along. However, a number of these are carried by the quarks themselves. In table 1 are given the quantum numbers of the three lightest quarks.
| quark | B |
Q |
J |
S |
I |
Iz |
| u | 1/3 | 2/3 | 1/2 | 0 | 1/2 | +1/2 |
| d | 1/3 | -1/3 | 1/2 | 0 | 1/2 | -1/2 |
| s | 1/3 | -1/3 | 1/2 | -1 | 0 | 0 |
Table 1: Quantum numbers of the quarks. B is baryon number, Q is electric charge, J is the spin, S is strangeness, I is the strong isospin and Iz is the projection of I along the quantization axis, (usually defined as z).
Building Mesons
In the constituent quark model, we treat a meson as a bound quark-antiquark pair,
 , and then draw an analogy to the positronium system,
e+e− to understand what we are seeing. In this
picture the
, and then draw an analogy to the positronium system,
e+e− to understand what we are seeing. In this
picture the  and the
and the 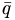 both have spin
both have spin 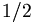 .
These can combine to either total spin
.
These can combine to either total spin 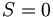 , or total spin
, or total spin 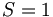 .
.
(1/(√ 2))[ ↑1 ↓2 - ↑2↓1 ] |
↑1↑2 |
In addition to the total spin, we can have orbital angular momentum L between the
 pair. Then, the L and S can combine to total angular momentum J = L ⊕ S, where J =| L−S |,| L−S+1 |,···,| L+S |. The states can be written in spectroscopic notation as 2S+1LJ, and are shown for positronium in table 2. Using the quarks as given in table 1, we are then able to use L, S and J to construct the JPC quantum numbers of the mesons.
pair. Then, the L and S can combine to total angular momentum J = L ⊕ S, where J =| L−S |,| L−S+1 |,···,| L+S |. The states can be written in spectroscopic notation as 2S+1LJ, and are shown for positronium in table 2. Using the quarks as given in table 1, we are then able to use L, S and J to construct the JPC quantum numbers of the mesons.
| State | S | L | J | P | C | JPC | Mesons | Name |
| 1S0 | 0 | 0 | 0 | - | + | 0-+ | π η η' K | Pseudoscalar |
| 3S1 | 1 | 0 | 1 | - | - | 1-- | ρ ω φ K* | Vector |
| 1P1 | 0 | 1 | 1 | + | - | 1+- | b1 h1 h1' K1 | Pseudo Vector |
| 3P0 | 1 | 1 | 0 | + | + | 0++ | a0 f0 f0' K*0 | Scalar |
| 3P1 | 1 | 1 | 1 | + | + | 1++ | a1 f1 f1' K1 | Axial Vector |
| 3P2 | 1 | 1 | 2 | + | + | 2++ | a2 f2 f2' K*2 | Tensor |
Table 2: The positronium states as a function of L, S and J. These then correspond to the named mesons of the specified JPC.
Parity
Let us start with parity, P. Mathematically,
parity is a reflection operator, and if the wave functions are eigenstates of the parity operator, thenP(ψ(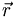 )) = ψ(
)) = ψ(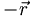 ) = ηP ψ(
) = ηP ψ(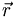 ).
).
Since applying parity twice should return us to the original state, the eigenvalues of parity, ηP can only be ±1. We can normally separate ψ into a radial and an angular piece,
ψ(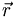 ) = R(r)Ylm(θ, φ).
) = R(r)Ylm(θ, φ).
In this case, the operation of parity leaves R unchanged, but transforms the angular
piece to Ylm(π − θ, φ + π), and it can be shown that:
Ylm(π − θ, φ + π) = (−1)lYlm(θ, φ).
Finally, fermions and antifermions have intrinsic opposite parity. This leads to the parity of a meson being:
P( ) = (−1)L+1 (1)
) = (−1)L+1 (1)
In considering that parity is conserved in a reaction, we consider the decay A → B+C, where there is orbital angular momentum l between B and C. Parity conservation says that
P(A) = P(B) · P(C) · (−1)l. (2)
C-Parity
The next quantum number is charge conjugation, C, which represents a trans- formation of the particle into its antiparticle. This reverses several properties of the particle such as charge and magnetic moment. Clearly, in order for a particle to be an eigenstate of the C operator, it must be electrically neutral. If we consider the π◦, then:
C|π◦ >=ηC |π◦ >
where ηC = ±1. If we imagine a meson built from a quark and its antiquark, say
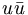 , with some total wave function of both its position and spin, Ψ.
, with some total wave function of both its position and spin, Ψ.
Ψ(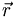 ,
, 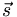 ) = R(r)Ylm(θ, φ)χ(
) = R(r)Ylm(θ, φ)χ(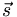 )
)
The charge conjugation operator acting on this state reverses the meaning of
u and 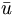 . This has the effect of mapping
. This has the effect of mapping 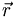 which points to the quark into
which points to the quark into 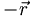 so that it continues to point at the quark. Under the same arguments that we used in parity, this leads to a factor (−1)L+1. This also flips the spin wave functions, leading to a factor of (−1) for the S=0 case and a factor of (+1) for the S=1 case. This is a factor of (−1)S+1, which when combined with the L factor leads to:
so that it continues to point at the quark. Under the same arguments that we used in parity, this leads to a factor (−1)L+1. This also flips the spin wave functions, leading to a factor of (−1) for the S=0 case and a factor of (+1) for the S=1 case. This is a factor of (−1)S+1, which when combined with the L factor leads to:
C( ) = (−1)L+S (3)
) = (−1)L+S (3)
G-Parity
Clearly charged particles cannot be eigenstates of C,
C | π+ >= η | π− >.
However, if we were to apply the C operator followed by a rotation in isospin,
R = exp(iπ I2 )
such that
| I, Iz > → | I, -Iz > ,
then charged particles could be eigenstates of this operator. We define the G parity operator as G = CR, and from this it is easy to show that for a  system,
system,
G = C · (−1)I.
These then lead to the following formulas.
J=L⊕S (4)
P = (−1)L+1 (5)
C = (−1)L+S (6)
G = (−1)L+S+I (7)
Quantum Numbers of Mesons
Using these relationships to build up possible JPC’s for mesons, we find that the following numbers are allowed:
0−+, 0++, 1−−, 1+−, 1−−, 2−−, 2−+, 2++, 3−−, 3+−,
3−−, · · ·and looking carefully at these, we find that there is a sequence of JPC’s which are not
allowed for a simple  system.
system.
0−−, 0+−, 1−+, 2+−, 3−+, · · ·
These latter quantum numbers are known as explicitly exotic quantum numbers. If a state with these quantum numbers is found, we know that it must be something other than a normal,  meson. Following the positronium analogy as in table 2, we can now assign the
JP(C) quantum numbers to the listed atomic states. In the case of mesons, we
have three quarks, u, d and s which can be combined with three antiquarks. This leads to
nine possible
meson. Following the positronium analogy as in table 2, we can now assign the
JP(C) quantum numbers to the listed atomic states. In the case of mesons, we
have three quarks, u, d and s which can be combined with three antiquarks. This leads to
nine possible  combinations with the same JP(C), rather
than the one positronium state.
combinations with the same JP(C), rather
than the one positronium state.
SU(3)
If we now assume that the three quarks are flavor symmetric, then we can use the SU(3)–flavor group to build up the nominal nine mesons, (a nonet).
3⊗3=1⊕8
The nine members of the nonet are going to be broken into two groups, eight members
of an octet, | 8 > and a single member of a singlet | 1 >. Under the SU(3) flavor
assumption, all the members of the octet have the same basic coupling constants
to similar reactions, while the singlet member could have a different coupling. The
nominal  combinations for the pseudoscalar mesons are shown
below. The three π’s are isospin I = 1, while the K’s are all isospin 1/2. The
| 1 > and | 8 > states are isospin 0.
combinations for the pseudoscalar mesons are shown
below. The three π’s are isospin I = 1, while the K’s are all isospin 1/2. The
| 1 > and | 8 > states are isospin 0.
| K0 | K+ | |||
| π- | π0,η,η' | π+ | ||
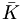 0 0 |
K+ |
In fact, the SU(3) quark content of the states is given as
(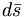 ) ) |
(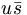 |
|||
(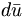 ) ) |
(1/√ 2)(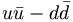 ) )(1/√ 6)(  ) ) |
(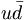 ) ) |
||
(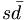 ) ) |
(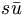 ) ) |
|||
(1/√ 3)( ) ) |
Naming of Mesons
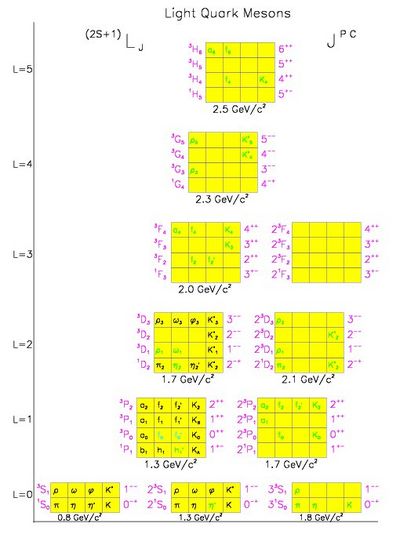
There is also a well prescribed naming scheme for the mesons as given in [caso98] which is summarized in table 3. This of course leads to an entire zoo of particles, but the name itself gives you all the quantum numbers of the state. If we put all of this together, we obtain an entire expected spectrum of mesons as shown in Fig. 1. Where no state is indicated, the meson has not been observed, while the dark names indicate well established states.
 |
Isospin | 1(Leven)J | 1(Lodd)J | 3(Leven)J | 3(Lodd)J |
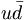 , ,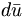 , ,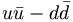 |
1 | πJ | bJ | ρJ | aJ |
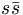 , ,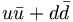 |
0 | ηJ,η'J | hJ,h'J | ωJ,φJ | fJ,f'J |
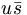 , ,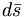 |
1/2 | JP=0-,1+... | KJ | JP=0+,1-... | K*J |
Mixing of I=0 States
Because the SU(3) flavor symmetry is not exact, the | 8 > and | 1 > states discussed above, (equation 9), are not necessarily the physical states. The two isospin zero states can mix to form the observed states. There is a bit of historical confusion about how the mixing should be written - enough so that it is worth discussing it. In an older reference, (e.g [close79]), the nonet mixing is written in terms of a mixing angle, θ, as follows in equation 10.
| f | cosθ | sinθ | |8> | ||
| = | (10) | ||||
| f' | −sin θ | cos θ | | 1 > |
In this parametrization, the so-called ideal mixing is given for cosθ=1/√3 and sinθ=√2/√ 3, or θ = 54.74◦. For this particular angle, the mixed states can easily shown to be as in equation 11.
f = (1/√ 2)(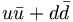 ) ) |
|
| (11) | |
f' = (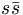 ) ) |
If one looks in the Particle Data Book [caso98], then the mixing is parametrized using a nonet mixing angle θn as in equation 12.
| f | cosθ | sinθ | |1> | ||
| = | (12) | ||||
| f' | −sin θ | cos θ | | 8 > |
In this scheme, the ideal mixing occurs for the choice of θn = 35.26◦, (cosθ = √2/√ 3, sin θ = 1/√ 3 ). Under this assumption, the physical states have the quark content as in equation 13. Most nonet mixing angles are now quoted in terms of this latter scheme, equation 12, and not in terms of equation 10.
f = (1/√ 2)(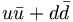 ) ) |
|
| (13) | |
f' = -(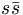 ) ) |
Mixing in the Pseudoscalar Sector
Finally, to make matters even worse, the 5 pseudo-scalar mesons are often written in a different mixing scheme [genz83]. One way to understand this is to imagine that the η and the η′ are interchanged, and that their names are the result of history (this is the approach taken by the pdg). In any case, in terms of the pseudo-scalar mixing angle, θP , their mixing is given as in equation 14.
| η' | cosθP | sinθP | |1> | ||
| = | (14) | ||||
| η | −sin θP | cos θP | | 8 > |
In the case of ideal mixing, θP = 35.26◦, it is the η which becomes an
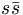 pair, and the η′ which becomes purely a light quark system.
Currently, the best value of the mixing angle is θP</sub> = −17◦. Using this angle, the η′ is
about 90% SU(3) singlet and the η is about 90% SU(3) octet. This can also be written in terms of the ideally mixed states as in equation 15, which shows the η′ as 62%
pair, and the η′ which becomes purely a light quark system.
Currently, the best value of the mixing angle is θP</sub> = −17◦. Using this angle, the η′ is
about 90% SU(3) singlet and the η is about 90% SU(3) octet. This can also be written in terms of the ideally mixed states as in equation 15, which shows the η′ as 62% 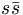 .
.
| η' | 0.61 | 0.79 | (1/√ 2)(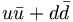 ) ) |
||
| = | (15) | ||||
| η | -0.79 | 0.61 | (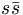 ) ) |
Mass Formulas
Finally, it is possible to use these SU(3) wave functions to predict mass relations between members of a meson nonet. For a pure nonet, one can derive a generalized linear mass formula, (equation 16). This formula is useful in predicting the masses of nonet members, and also verifying that a set of states can actually form a nonet.
(mf +mf′)(4mK −ma)−3mfmf′ =8mK2 −8mKma +3ma2. (16)
In addition to the linear mass formula, it is also possible to predict the nonet mixing angle, θn purely from the masses. Equation 17 can be used to determine the mixing angles, and when applied to three well established nonets, we find the mixing angles given in table 4. What is particularly interesting is that the three nonets are all reasonably close to ideally mixed. It appears that in many situation, nature wants to separate the light quarks,
(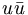 and
and 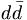 ) from the heavier s–quarks, (
) from the heavier s–quarks, (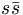 ).
In fact, there are only two clear situation where this angle appears not to be ideally mixed. The ground state pseudoscalar mesons, where other effects are important, and the scalar mesons, where a glueball may be mixed into the nonet. If there are other nonets which are not ideally mixed is an open and important question.
).
In fact, there are only two clear situation where this angle appears not to be ideally mixed. The ground state pseudoscalar mesons, where other effects are important, and the scalar mesons, where a glueball may be mixed into the nonet. If there are other nonets which are not ideally mixed is an open and important question.
tan2θn=(3mf′ −4mK+ma)/(4mK-ma-3mf) (17)
Figure 1. The expected meson spectrum showing the 2S+1LJ representation, the JPC of the nonet, and the names of the states. Along the vertical axis are plotted nonets for increasing values of L, while along the horizontal are plotted radial excitations. The average masses are indicated under the boxes. Dark names indicate well established states, while the lighter names are tentative assignments. All other states have not yet been observed, (File:Meson.pdf).