Guide to Monte Carlo event timing and detached vertices in HDGeant/4
Contents
Conceptual overview
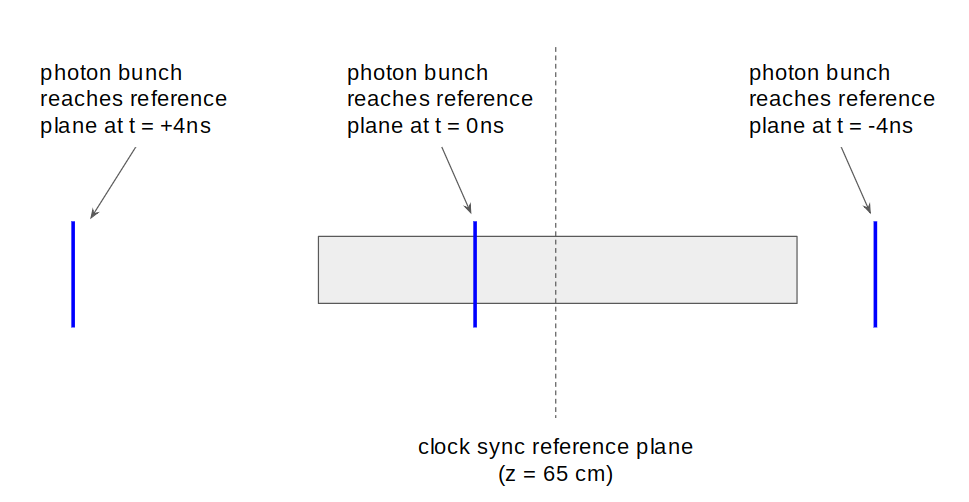
Event vertex timing in the hdgeant/hdgeant4 simulation is illustrated in the figure above. The blue lines represent the planar wavefronts of the photon beam pulse structure, and the gray box represents the liquid hydrogen target. The target mid-plane at z=65cm has been defined as the simulation clock reference plane, so that the clock ticks every time a photon pulse passes through that plane. That is all you are allowed to know about the t=0 of the simulation clock. In the real experiment, you do not know a proiri which pulse contained the gamma that generated the interaction, all you know is that it was one of this discrete set within some dozen or so of the bunch that the event trigger time points to. After track vertexing, you can figure that out, but from the clock alone you cannot know anything more than this. Thus, the simulation is designed to obscure the true reference time of the interaction vertex, so that you have to work it out in the reconstruction and analysis in just the same way.
Of course, the obscuring of truth information in the simulation is not complete. If you want to cheat, you can inspect the Monte Carlo record in each simulated event and find out what the exact time was of the primary interaction vertex. Below I give an example of an event from an external Monte Carlo event generator that has been prepared for input to hdgeant/hdgeant4. This particular event might represent a heavy photon produced in the target and decaying to e+e- some distance from the primary vertex. The units of distance are cm, time is ns, and momentum/energy are GeV.
<HDDM class="s" version="1.0" xmlns="http://www.gluex.org/hddm">
<geometry md5reconstruction="" md5simulation="" md5smear="" />
<physicsEvent eventNo="1" runNo="42553">
<reaction type="0" weight="0">
<beam type="Photon">
<momentum E="0.0143928" px="-5.79431e-08" py="1.6068e-07" pz="0.0143928" />
<polarization Px="0.0477761" Py="-0.062995" Pz="8.95607e-07" />
</beam>
<vertex>
<product decayVertex="1" id="1" mech="0" parentid="0" pdgtype="0" type="Unknown">
<momentum E="11.6002" px="-0.00026237" py="-6.82093e-05" pz="11.6002" />
</product>
<origin t="0" vx="0" vy="0" vz="0" />
</vertex>
<vertex>
<product decayVertex="0" id="2" mech="1447972675" parentid="1" pdgtype="-11" type="Positron">
<momentum E="0.00367671" px="-0.000451987" py="-0.000230665" pz="0.0036055" />
</product>
<product decayVertex="0" id="3" mech="1447972675" parentid="1" pdgtype="11" type="Electron">
<momentum E="0.0107161" px="0.000553506" py="-0.00110481" pz="0.0106324" />
</product>
<origin t="1.01" vx="-0.582" vy="0.004" vz="8.776" />
</vertex>
<random seed1="1078571841" seed2="1576092742" seed3="709975946" seed4="912931182" />
</reaction>
</physicsEvent>
</HDDM>
The primary vertex is always the one with decayVertex="0", which should be the first one in the vertex tag sequence. The meaning of the generated event structure above should be more or less obvious. Here we focus on the <origin> tags, where all of the information about event vertexing and timing is located.
Vertex position
The primary vertex in this example is given an origin with zero position. This is normally the location of the primary vertex within the target volume, but if you set all three components to zero then a random position will be generated by hdgeant/hdgeant4 within the beam-target overlap volume, and the entire event shifted to place the origin there. There must always be one primary vertex per physics event. If there are secondary vertices that need to be specified by the Monte Carlo generator, give these decayVertex>0, as in the example above, and specify in their origin tag the time and position of the detached vertex relative to the primary vertex. In the above example, the Unknown particle travels a distance 8.8cm downstream from the primary vertex, where it decays into e+,e- after 1.01 ns. When the primary vertex is randomized inside the beam-target interaction volume, all vertices are shifted by the same amount.
Vertex time
The interpretation of the t attribute of the origin tag is a bit more complicated. The meaning is different in the input record that is fed to hdgeant/hdgeant4 from an external event generator, and the value that the same attribute contains when the event is written to the simulation output. The most important thing to understand in this context is how the simulation clock is synchronized with the beam: t=0 in the simulation corresponds to one of the photon wavefronts in the beam passing through the reference plane at z=65cm. This means that if the primary vertex were at 95cm (would be outside the target!) then the vertex time would be 1ns, or 5ns, or 17ns, or -11ns. Which one of these possibilities gets selected is randomized for each event in the simulation, so as to mimic the time uncertainty in the real event trigger. This complication is really outside the scope of event generators, which should focus instead on specifying the internal event topology. If the generator simply writes t=0 in the origin tag for its primary vertex in its hddm output, the simulation will take care of assigning the vertex times according to the beam bunch structure. When the same event is written out by hdgeant/hdgeant4, the t value in the origin tag of the vertices are all overwritten with the actual values that were used in the simulation. Thus, an event with the primary vertex origin t=0 will come out of the simulation with a non-zero primary vertex origin t value. This case is illustrated in the example given above. On the other hand, if you prefer to control the vertex timing in your event generator, you can assign non-zero origin t values for the primary vertex in your generated events, and the simulation will simply adopt your value unmodified. This mimics the behavior it has when a non-zero vertex position is specified in the generated events. The rule is this: If you want to control the vertex position [time], set its origin vector [t] to a non-zero value. If you want to let the simulation take care of assigning an appropriate vertex position [time] then set your origin vector [t] to zero in your generator output, and the zeros will be overwritten by hdgeant/hdgeant4 with the generated values in the output record. Note that if you specify non-zero values for your vertex origin times, your values will be adopted without checking if they align with the beam bunch structure. Be warned that if you do this, tagging accidentals subtraction will not work correctly unless you have computed your vertex times with the beam structure in mind.
Setting t=0 in the primary vertex is almost always the correct thing to do in your event generator. To see where that ends up on the simulation clock, run it through hdgeant/hdgeant4 and look at the origin t-value in the output MC record from the simulation. Below is what the above example event record looks like after running it through hdgeant4. Notice that only the <origin> tag has changed between the above printout and the one below. The hitView section has been suppressed in this printout.
<HDDM class="s" version="1.0" xmlns="http://www.gluex.org/hddm">
<geometry md5reconstruction="" md5simulation="eb0f31e2970cfcd67a51371a6dbf2216" md5smear="" />
<physicsEvent eventNo="1" runNo="42553">
<reaction type="0" weight="0">
<beam type="Photon">
<momentum E="0.0143928" px="-5.79431e-08" py="1.6068e-07" pz="0.0143928" />
<polarization Px="0.0477761" Py="-0.062995" Pz="8.95607e-07" />
</beam>
<vertex>
<product decayVertex="1" id="1" mech="0" parentid="0" pdgtype="0" type="Unknown">
<momentum E="11.6002" px="-0.00026237" py="-6.82093e-05" pz="11.6002" />
</product>
<origin t="-12.2361" vx="-0.130076" vy="0.185582" vz="58.0447" />
</vertex>
<vertex>
<product decayVertex="0" id="2" mech="1447972675" parentid="1" pdgtype="-11" type="Positron">
<momentum E="0.00367671" px="-0.000451987" py="-0.000230665" pz="0.0036055" />
</product>
<product decayVertex="0" id="3" mech="1447972675" parentid="1" pdgtype="11" type="Electron">
<momentum E="0.0107161" px="0.000553506" py="-0.00110481" pz="0.0106324" />
</product>
<origin t="-11.2461" vx="-0.712076" vy="0.189582" vz="66.8207" />
</vertex>
<random seed1="1078571841" seed2="1576092742" seed3="709975946" seed4="912931182" />
</reaction>
</physicsEvent>
</HDDM>
Special considerations with delayed vertices
One mistake that is easy to make when generating events with delayed vertices specified in an external Monte Carlo generator is that of double-counting the final-state particles. In the above example, there is no double-counting because the unstable intermediate particle is of untrackable type="Unknown". But what if instead I had given the particle from the primary vertex the type="Photon"? Then hdgeant/hdgeant4 would have tracked that photon, which would go off somewhere into the forward part of the detector and create a shower, then it would have come back and tracked the electron-positron pair. In general, every particle with a <product> tag inside a <vertex> element that has a type known to Geant3/Geant4 is tracked independently by the simulation. If you want to keep the information about the intermediate particles in an explicit decay chain, but not have hdgeant/hdgeant4 track them, assign them a type that is unknown to Geant3/Geant4, that is with type<=0. Any negative type value maps to Unknown, so you can retain a private catalog of many kinds of intermediate particles known to your event generator, indexed by negative integer type values.