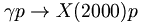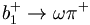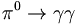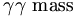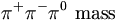Difference between revisions of "Mark's Sandbox"
m (Text replacement - "Unit vector along the line" to "The unit vector along the line") |
|||
| (17 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | [[Converting sim-recon tags and branches to halld_recon or halld_sim tags and branches]] | ||
| + | |||
| + | <html><img src="https://avatars1.githubusercontent.com/u/5664701?s=40&v=4"></html> | ||
| + | |||
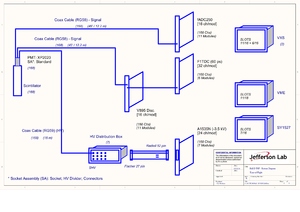
[[Image: Electronics Time of Flight.png|thumb|TOF electronics chain]] | [[Image: Electronics Time of Flight.png|thumb|TOF electronics chain]] | ||
| + | [[Image:Cpu-usage-271x260.jpg]] | ||
* <math>\gamma p\rightarrow X(2000)p</math> | * <math>\gamma p\rightarrow X(2000)p</math> | ||
| Line 17: | Line 22: | ||
Suggested coordinate system for linear detector elements in a plane perpendicular to z. | Suggested coordinate system for linear detector elements in a plane perpendicular to z. | ||
| − | Assume line direction is chosen to go in the positive $y$ direction. If the line is parallel to the x-axis, choose the positive direction to be the positive x direction. Then the angle of inclination of the line is an angle $\phi$, 0 <= phi < 180. The unit vector along the line is lhat = xhat cos phi + yhat sin phi, the unit vector normal to the line (in the detector plane) is nhat = -xhat sin phi + yhat cos phi. In this way, lhat and nhat satisfy the right hand rule, i. e., lhat cross nhat = zhat. | + | Assume line direction is chosen to go in the positive $y$ direction. If the line is parallel to the x-axis yo, choose the positive direction to be the positive x direction. Then the angle of inclination of the line or lines is an angle $\phi$, 0 <= phi < 180. The unit vector along the line is lhat = xhat cos phi + yhat sin phi, the unit vector normal to the line (in the detector plane) is nhat = -xhat sin phi + yhat cos phi. In this way, lhat and nhat satisfy the right hand rule, i. e., lhat cross nhat = zhat. |
| − | * [[test of | + | * [[test of wiki tranformation of coding standards]] |
| − | * [[ test of | + | * [[ test of wiki tranformation of coding standards | text ]]. |
| − | * [[test of | + | * [[test of wiki tranformation of coding standards|text]]. |
* [[Getting a Grid Certificate]] | * [[Getting a Grid Certificate]] | ||
| Line 27: | Line 32: | ||
* as a test | * as a test | ||
| − | <img src="https:// | + | <img src="https://halldweb.jlab.org/wiki/images/5/5b/D00000-01-01-2000.png"> |
[[Simple Email Lists]] | [[Simple Email Lists]] | ||
| Line 39: | Line 44: | ||
--[[User:Marki|marki]] 17:23, 6 October 2014 (EDT) | --[[User:Marki|marki]] 17:23, 6 October 2014 (EDT) | ||
| + | |||
| + | add another image here: [[file:Tunnel2.jpg]] | ||
| + | |||
| + | new image [[image:test.jpg]] before this | ||
| + | Additional text | ||
| + | A test private page: [[Private: Test Private Page]] | ||
| + | test of link to private wiki: [[privatewiki:Mark's Sandbox]] | ||
| + | |||
| + | <table><tr><td>a<td>b<tr><td>c<td>d</table> | ||
| + | |||
| + | <html><iframe src="https://calendar.google.com/calendar/embed?height=300&wkst=1&bgcolor=%23FFFFFF&src=503o985nbesua43smquc510o8k%40group.calendar.google.com&color=%23875509&src=halldops%40gmail.com&color=%2323164E&ctz=America%2FNew_York" style="border-width:0" width="400" height="300" frameborder="0" scrolling="no"></iframe></html> | ||
| + | |||
| + | = H1 = | ||
| + | == H2 == | ||
| + | === H3 === | ||
| + | ==== H4 ==== | ||
| + | ===== H5 ===== | ||
| + | ====== H6 ====== | ||
Latest revision as of 14:36, 24 February 2021
Converting sim-recon tags and branches to halld_recon or halld_sim tags and branches

random text forming a paragraph
Suggested coordinate system for linear detector elements in a plane perpendicular to z.
Assume line direction is chosen to go in the positive $y$ direction. If the line is parallel to the x-axis yo, choose the positive direction to be the positive x direction. Then the angle of inclination of the line or lines is an angle $\phi$, 0 <= phi < 180. The unit vector along the line is lhat = xhat cos phi + yhat sin phi, the unit vector normal to the line (in the detector plane) is nhat = -xhat sin phi + yhat cos phi. In this way, lhat and nhat satisfy the right hand rule, i. e., lhat cross nhat = zhat.
- here are some new bullets
- as a test
<img src="https://halldweb.jlab.org/wiki/images/5/5b/D00000-01-01-2000.png">
here is an edit
--marki 17:23, 6 October 2014 (EDT)
new image ![]() before this
Additional text
A test private page: Private: Test Private Page
test of link to private wiki: privatewiki:Mark's Sandbox
before this
Additional text
A test private page: Private: Test Private Page
test of link to private wiki: privatewiki:Mark's Sandbox
| a | b |
| c | d |