Track Finding/Fitting 2006
Contents
May 22, 2006
In preparation for the GlueX presentation at PAC 30, I have started looking at what kind of tracking resolutions can be obtained from the current GlueX track finding code. This is built on the earlier work documented in [GlueX Note 528] .
It is important to note that the goal of the code used here is to find tracks and give initial parameters for input to the final (Kalman) fitter. The final fitter is not yet written. Resolutions obtained from the simple helical fits of the track finder are useful for:
- Upper limits on tracking resolutions
- Resolutions seen by Level-3 trigger
Non-uniform B-field
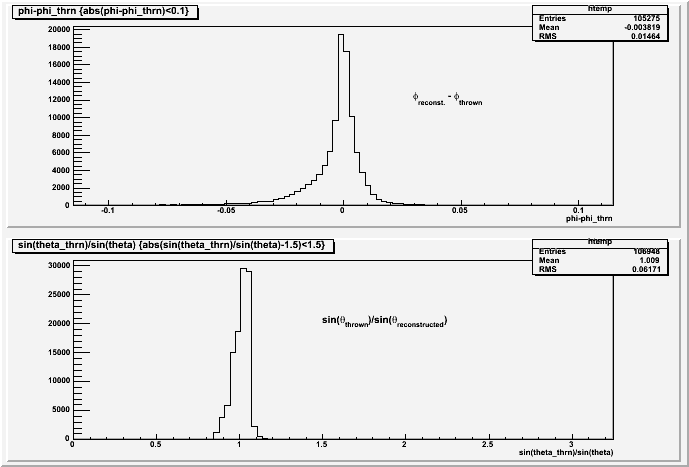
One of the problems with the current tracking code is that it is not terribly accurate at determining the particle's momentum. This is because the fit is a pure helix and the momentum is derived from the radius of the helix (and the theta angle). In other words, using a helix assumes a uniform, constant magnetic field. When an inhomogeneous field map is used, the angles of the particle at the vertex (phi and theta) are reconstructed reasonably well as shown in the next plot.
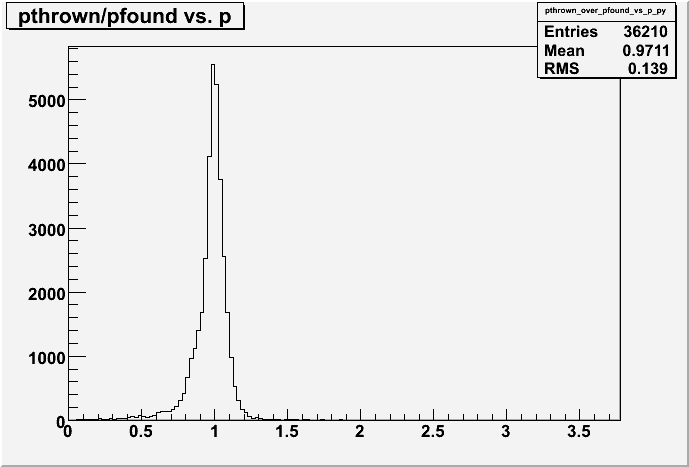
The momentum magnitude, however, is not as shown here:
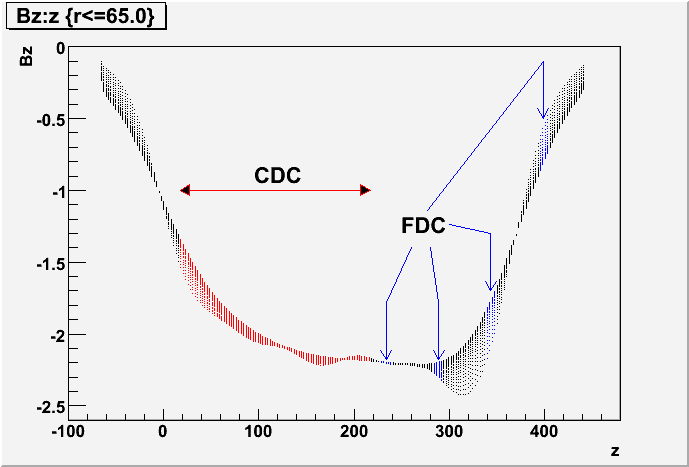
This next plot shows the z-component of the magnetic field as a function of z (along the beamline) in cm. The values of Bz are plotted for distances from the beamline(R=0) out to the BCAL (R=65cm). The locations of the CDC and FDC packages are shown. From this you can see that the field drops dramatically between the first and last FDC package.