Track Finding/Fitting 2006
Contents
May 22, 2006
In preparation for the GlueX presentation at PAC 30, I have started looking at what kind of tracking resolutions can be obtained from the current GlueX track finding code. This is built on the earlier work documented in [GlueX Note 528] .
It is important to note that the goal of the code used here is to find tracks and give initial parameters for input to the final (Kalman) fitter. The final fitter is not yet written. Resolutions obtained from the simple helical fits of the track finder are useful for:
- Upper limits on tracking resolutions
- Resolutions seen by Level-3 trigger
Non-uniform B-field
One of the problems with the current tracking code is that it is not terribly accurate at determining the particle's momentum. This is because the fit is a pure helix and the momentum is derived from the radius of the helix (and the theta angle). In other words, using a helix assumes a uniform, constant magnetic field. When an inhomogeneous field map is used, the reconstructed parameters aren't so accurate as shown in the following plots:
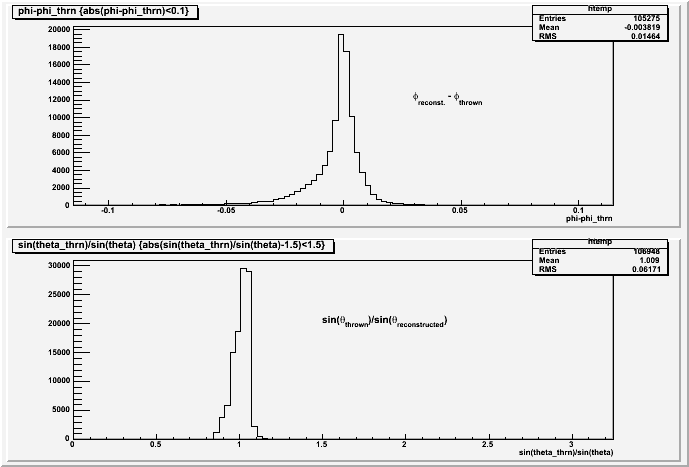
Here are the reconstructed angles (phi, theta) of single pi+ events with energies ranging from 200MeV to 9GeV. The top plots shows the difference between thrown and reconstructed phi angle in radians. The bottom plot shows the ratio of sin(theta_thrown) to sin(theta). The ratio of sin(theta)s are plotted since the total momentum is calculated by dividing the transverse momentum by sin(theta).
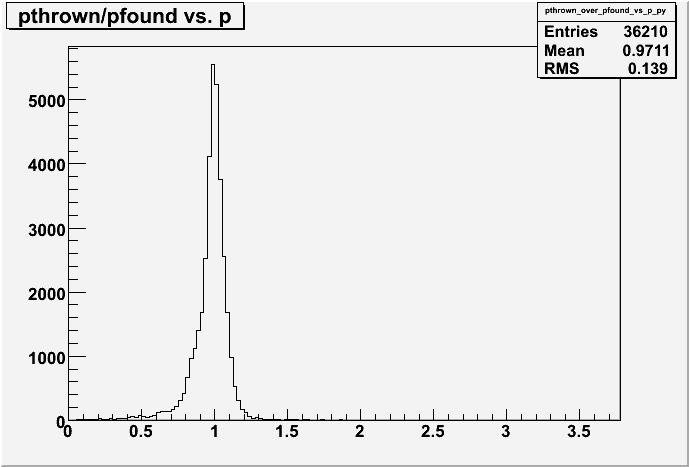
The following plot shows the ratio of total momentum, thrown to reconstructed.
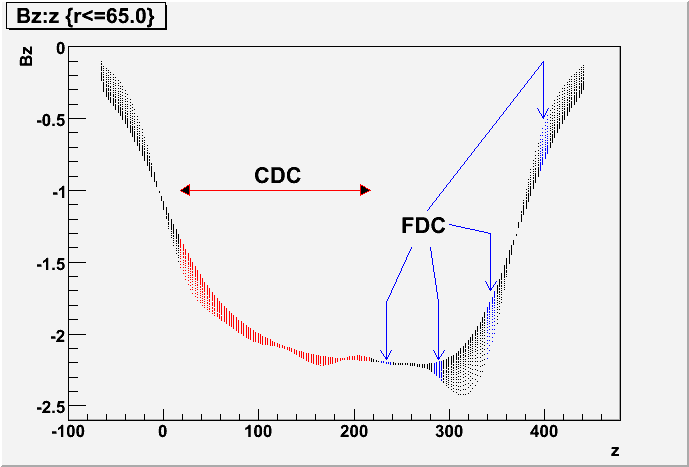
This next plot shows the z-component of the magnetic field as a function of z (along the beamline) in cm. The values of Bz are plotted for distances from the beamline(R=0) out to the BCAL (R=65cm). The locations of the CDC and FDC packages are shown. From this you can see that the field drops dramatically between the first and last FDC package.
Helical Parameters
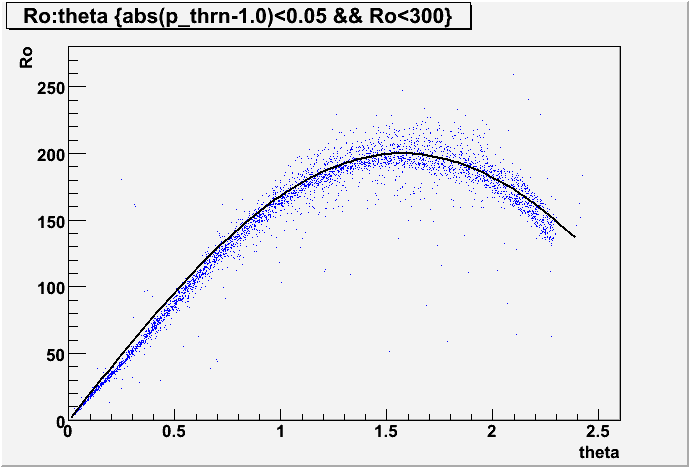
Extracting the total momentum from the helical parameters cannot lead to a resolution better than what is in the parameter space itself. Take for example the following plot. This plot was generated by thowing 1.0GeV pi+ particles isotropically in hdgeant and fitting the resulting track hits to a helix. The plot is the of the radius of the helix (Ro) vs. the theta angle in radians. Since all of the thrown particles had the same momentum, the value of Ro, which is proportional to the transverse momentum, should go like sin(theta). At least, that would be the case for a uniform magnetic field in vacuumm. Overlayed on this plot is a sine function with the appropriate amplitude. One can see that the curve generally fits, but not perfectly.
Uniform vs. Non-uniform Magnetic Fields
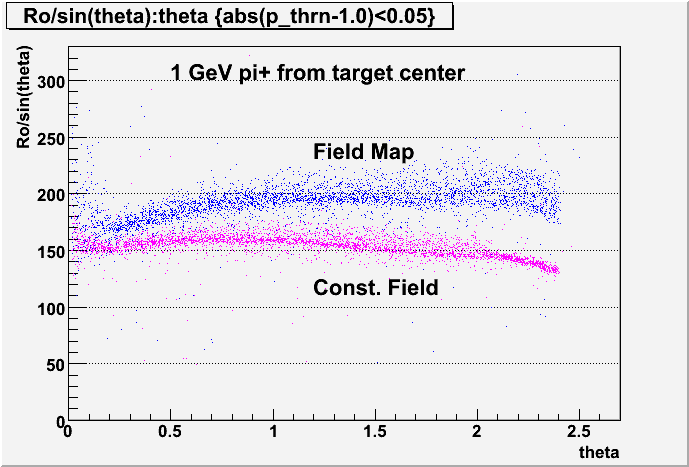
The following plot is similar to the preceding one except the Y-axis is Ro/sin(theta) instead of just Ro. This means for the ideal case, the value along Y is proportional to the momentum. In other words, since all tracks had the same momentum, this should be a horizontal line. The two curves indicate using a constant -2.2T magnetic field in hdgeant and an inhomogeneous magnetic field from the standard GlueX solenoid map. One can see that even for the constant magnetic field, the curve is not flat. Presumably, this is due primarily to energy loss and multiple scattering.