Detector Rates and Lifetime
As the rates close to the photon beam line can be substantial it is necessary to investigate the consequences on the performance and lifetime of the scintillator itself and its readout devices.
Contents
Rate Estimates
The estimated rates in a given paddle depend on the upstream detector geometry and target material. Some estimates can be found in GlueX-DB 1471. In figure 7 on page 9 of this document you find the estimated rates for all paddles with the half sized paddles on the side (41 - 44). The rates for the central paddles are expected to be rather large up to 12 MHz! These are calculations with 6cm wide paddles of 1 inch thickness. Therefore splitting the central paddles in half is a necessity to cut down the rates to a more acceptable level.
PMT specifications
According to the specifications for the Hamamatsu PMT H9779 (8-stage) the maximum operating current is 0.1 mA. Elton estimated the signal amplitude based on this maximum current assuming a gain of 5*10^5 and 50ns signal base line. This results in an amplitude of 50mV. From bench tests with an LED on an H10534 PMT assembly with a 10-stage H9779 PMT and operating voltage of 1900V resulting in a gain of 4.1*10^6 and a measured 270 photo electrons per LED pulse a signal amplitude of 1.45V was recorded. The signal base line was about 20ns. Assuming a triangular signal shape the total charge of the signal is 0.5 * 1.45V * 20*10^-9s / 50Ohm = 2.9*10^-10 C. At a rate of 3MHz this would correspond to a current of 0.9 mA!
Rate and Current calculations
The basis of this estimate is GlueX-Doc 1471 figure 6 and 7. The following is an energy spectrum of a tof paddle for the expected electromagnetic background.

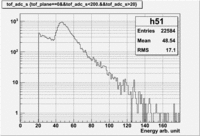
The peak around 50 represents the photons that convert at the entrance to the TOF paddle or before thereby looking like a MIP particle. The shape of the peak is a typical Landau distribution. The mean of this peak (ADC=54) is approximately the mean energy loss of MIPs in plastic scintillator (2MeV/cm) and amounts to about 5MeV.
At zero threshold the mean of the full distribution is about 32. And corresponds to a rate of about 16MHz for the innermost paddle according to figure 8 of GlueX-Doc 1471. In order to estimate the current in the PMT for such a situation several assumptions need to be made:
- Signal base line 25ns
- Signal shape triangular
- Signal amplitude for mean MIPs (ADC=54) 1000mV
- Load 50 Ohms
- Rage at zero threshold 16MHz
Here it is assumed that the HV of the PMT is set such that the mean energy loss of MIPs results in a 1Volt signal amplitude. The mean charge for a zero threshold is then given as
Q = 32./54 * 1/50Ohms * 25ns * 1/2 = 0.148 *10^-9
with a rate of 16MHz this results in a current of
I = Q*16MHz = 0.148 *10^-9 * 16*10^6 = 2.37 mA
This is a factor of about 24 higher than the maximum recommended current for the PMT of 0.1mA!
Reduce Rates and Current
For the innermost paddle where a full background rate of about 16MHz is expected at zero threshold, it is unavoidable to reduce the size of the paddles to reduce these very high rates. Reducing the width of the paddle by two will roughly cut the rate in half. Therefore such paddles will see a maximum rate of about 8MHz. At such a rate the current will still be far to high (factor 12) and it is necessary to reduce the current by reducing the signal amplitude. This can be achieved by reducing the gain. This means the operating high voltage is considerably smaller and it is important to see weather the voltage divider is still adequate for this lower HV. It is important to maintain a sufficiently large voltage drop between the photo cathode and the first dynode to ensure good timing. So at low operating voltage the choice of resistors may need to be reconsidered. This may also be true with respect to the last dynode.
In the situation at hand the mean signal amplitude for MIPs will need to be below 100mV and an amplification of the signal of about 5 to 10 has to be applied preferentially at the location of the divider. Such an amplification could be part of the base.
According to figure 7 in GlueX-Doc 1471 such a designed is probably required for the PMTs of the first 3 full paddles close to the beam line with the first paddle being split in half to make two paddles with 30mm width each. The four half paddles with only one PMT each should also have bases in this manner. The remaining paddles of the TOF see sufficiently low rates and can be operated with standard PMT bases.
Monte Carlo results
Monte Carlo data has been generated similar to GlueX-Doc 1471 to further investigate the issue of rates in the TOF detector. First we look at the relative rates between paddles by looking at the paddles hit distribution shown in the following plot:
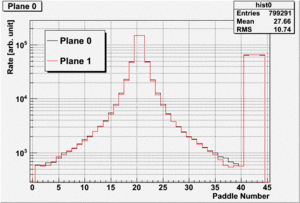
Paddle number 20 is the long paddle (two sided readout) closest to the beam hole. The rate from electromagnetic background is 16MHz at high luminosity according to GlueX-Doc 1471. A first step in reducing this rate in this paddle
is by splitting it in half make it two paddles of 3cm width each. What is also easy to see is that at the location of the fourth paddle the rate is about a factor of 10 less. At the location of paddle 15 (sixth from the center) the rade is reduced by a factor of 15.
The second important characteristic to know about this electromagnetic background is the energy distribution created in the TOF paddles. This is shown in the following figure:
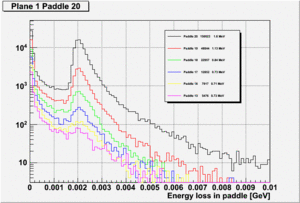
Paddle 20 is the closed paddle to the beam hole (black curve). The first number in each line represents the total integral of hits in each histogram. The second number is the mean energy deposition in the histogram. The bump at 2 MeV follows a Landau distribution resulting from minimum ionizing charged particles.
Note: This is not the true energy loss of MIPs in the paddle but the attenuated one. So this is equivalent to the light the PMT will see!
If we assume a 16MHz for the inner most paddle(black curve) then we expect for the second paddle (red curve) rate of 16MHz/150023*48844 = 5.2MHz
The mean current due to this background in the PMT is directly related to the mean of the distribution.
Because the mean of the distribution drops from 1.6 MeV to 1.13 MeV the expected mean current in the PMT will be lower than just what is expected from the reduced rate from 16MHz to 5.2MHz.
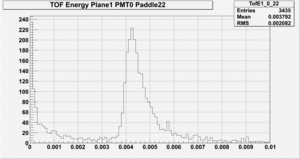
Next 5 GeV/c pi+ mesons are generated from the down stream end of the target. The polar angle is chosen such that these
particles will just pass by the down stream edge of the BCAL and hit the TOF at large angles. The hits will be close to one PMT and far from the other PMT. The hist are about 107 cm from the center of the paddle. So about 18 cm from the close end and 233 cm from the far end. In the following plots the unit of the horizontal axis is in GeV.
Close end PMT energy spectrum:
Far end PMT energy spectrum:
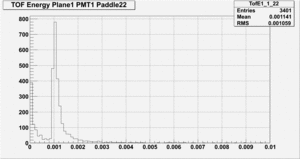
From the the far PMT energy spectrum one can see that the threshold has to be sufficiently low for these energy signals to generate a discriminator output. In this case the threshold needs to be as low as 0.8 MeV or even lower. This means the threshold for the closes paddle to the beam line needs to be about a factor of two lower than the mean energy deposition of the electromagnetic background that causes the high rates. For a paddle further away from the beam line the mean energy deposition from electromagnetic background is only about 0.7 MeV which is already lower than minimum threshold of 0.8 MeV. Of course if the threshold can be set lower this would be preferable.
The following table is a list of the high rate paddles and what current to expect if the gain of the PMT is set such that the mean of the electromagnetic background is set to be at 100mV signal amplitude. Note that as a consequence of this choice the gain for each PMT is different!
| Paddle # | EM backgr. Rate MHz | Mean EM bckgr. MeV | Central MIP mV | PMT cur. [100mV] |
|---|---|---|---|---|
| 20 | 16 MHz | 1.6 MeV | 165 mV | 0.400 mA |
| 19 | 5.2 MHz | 1.2 MeV | 208 mV | 0.130 mA |
| 18 | 2.1 MHz | 0.84 MeV | 298 mV | 0.053 mA |
| 17 | 1.6 MHz | 0.73 MeV | 342 mV | 0.040 mA |
| 16 | 1.0 MHz | 0.71 MeV | 352 mV | 0.025 mA |
Operating PMT at 0.02mA
According to the manufacturer of the PMT operating it at a current of 0.1mA will cause a drop in gain of 50% after 1000 hours of operation.
It is therefore recommended to adjust the gain such that the operating current is well below this value. In the following I assume an operating
current of 0.02mA and calculate the expected signal amplitudes for different TOF paddles.
Additional assumptions are
1) Signal base line 40ns
2) Signal shape triangular
3) NO 50 Ohm termination at the base
4) PMT current 0.02mA
From this it follows:
h[V]*1/2*40*10^(-9)[s]/50[Ohm] * RATE = 0.02[mA]
In the above equation "h" is the signal amplitude in Volts and "RATE" is the detector rate in Herz. Solving for "h" gives the following:
h = 5*10^(4)/RATE
In the following table the numbers are for the low intensity data taking:
| Paddle | Rate [MHz] | Mean dE [MeV] | Signal Mean [mV] | Signal Max [mV] | Signal Min [mV] |
|---|---|---|---|---|---|
| 3cm | 1.0 | 1.6 | 50 | 140 | 28 |
| 3cm | 0.6 | 1.6 | 83 | 224 | 46 |
| 6cm | 0.5 | 1.2 | 100 | 375 | 75 |
| 6cm | 0.2 | 0.85 | 250 | 1323 | 265 |
In the table above it is assumed that the gain of the PMT is set such that it draws a current of 0.02mA through the anode. For the 3cm wide full length paddle closest to the beam line a rate of about 1MHz is expected at low luminosity. Note, this is an estimate not a number derived directly from Monte Carlo simulations. The smallest signal expected in such a paddle when a minimum ionizing particle is hitting the far end is about 28mV. For the next paddle of the same width the gain can be set higher so that the smallest signals are expected to be about 75mV. Assuming a Threshold of 20mV there is only the innermost half width paddle that needs to be operated at a gain that will exceed the 0.02mA current limit assumed above. Doubling the current limit will lead to a doubling in gain and hence in a doubling in signal amplitude for this paddle to about 56mV. This wold be almost a factor of 3 above an assumed threshold of 20mV.
It is estimated that a MIP passing through the center of the paddle will generate in average 2138 photo electrons in the PMT. This corresponds to an average 2.5MeV energy deposition seen by the PMT (after attenuation) determined from Monte Carlo. For the innermost paddle with the highest rate this corresponds to a signal amplitude of 78mV. From this we deduct the PMT gain to be 1.8*10^5. For the next neighbouring paddle we expect a signal amplitude of about 130mV for these events resulting in a gain of 3.0*10^5 and for the first full width paddle and an expected signal amplitude of 208mV a gain of 4.8*10^5 is estimated.
The Hamamatsu PMT R9779 8-stage tube has a gain of 5.*10^5 at an operating voltage of 1500 Volts. At the maximum recommended operating voltage of 1750 the gain of the tube is slightly above 1.0*10^6. According to these numbers the 8-stage PMT is what is needed for the central TOF paddles. However this PMT seems to be also sufficient for all other paddles because operating them at a gain of about 5*10^5 provides reasonable large signals according to the above estimates.