GlueX Physics Strong Decay Models
Contents
GlueX Physics
Review Papers
Mesons in the Quark Model
Exotic Quantum Number Mesons
Lattice QCD Calculations
Photoproduction
Strong Decay Models
SU(3) Decay Calculations
SU(3) Rules
A simple starting point for looking at decays of mesons is to consider SU(3) flavor symmetry in the light-quark (u,d,s) sector. As we saw in the earlier section on SU(3), mesons are arranged in nonets (nine) of  pairs, with these in turn being broken into an SU(3) singlet state and eight SU(3) octet states. If we consider the decay of a meson to pairs of mesons, where both daughters are members of the same nonet (e.g. the pseudoscalar mesons), then we can use SU(3) algebra to determine
which decays are possible.
pairs, with these in turn being broken into an SU(3) singlet state and eight SU(3) octet states. If we consider the decay of a meson to pairs of mesons, where both daughters are members of the same nonet (e.g. the pseudoscalar mesons), then we can use SU(3) algebra to determine
which decays are possible.
In SU(3), we note that the product of an 8 times an 8 is given as the sum:
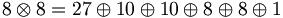
Thus, it is possible for a pair of octet mesons to couple to an octet meson or a singlet meson
(the 27 and the 10 do not represent simple  systems). Similarly,
under SU(3)
systems). Similarly,
under SU(3)
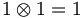
and
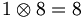 .
.
Putting all of this together, there are four types of decays that we see could be allowed under SU(3). Each of these could, in principle, have its own decay constant
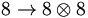 |
gT | (1) |
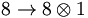 |
g18 | (2) |
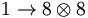 |
g1 | (3) |
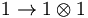 |
g11 | (4) |
Decay Rates
In the following, we will show that under the assumption that some decays are forbidden, we can reduce the four constants gT, g18, g1, g11 down to one unknown constant per nonet.
The decay rate 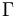 can be expressed as
can be expressed as
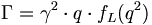 (5)
(5)
where q is the break-up momentum from the decay of 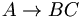 . In the rest-frame of A, both B and C have momentum q, with
. In the rest-frame of A, both B and C have momentum q, with
![q={\frac {[(m_{A}^{2}-(m_{B}+m_{C})^{2})\cdot (m_{A}^{2}-(m_{B}-m_{C})^{2})]^{{(1/2)}}}{2m_{A}}}](/wiki/images/math/9/7/e/97eef0fbc16b927463f8a441dbdae2dc.png)
The momentum q is related to the available phase-space for the decay to occur,
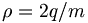 . In addition to the phase-space factor, q, we can also have a form factor for the decay, fL(q). This can depend on the break-up momentum as well as the orbital angular momentum between B and C (L).
. In addition to the phase-space factor, q, we can also have a form factor for the decay, fL(q). This can depend on the break-up momentum as well as the orbital angular momentum between B and C (L).
SU(3) Clebsch-Gordan Coefficients
In order to compute the decay rates, we will now take advantage of the SU(3) Clebsch-Gordan (c.g.) coefficients. For the decay 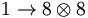 , we can express the individual decays as
, we can express the individual decays as
(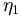 ) ) |
 |
![[(K^{+},K^{0}){\bar K},(\pi ^{+},\pi ^{0},\pi ^{-})\pi ,\eta _{8}\eta _{8},(K^{-},{\bar K}^{0})K]](/wiki/images/math/0/1/4/01473a5156419d74fb77d9046ca9dd24.png) |
where the corresponding four c.g coefficients are given by
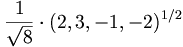 , , |
where it is implicitly taken that the minus sign inside the square root is factored out front.
Thus
=-1/{\sqrt {8}}](/wiki/images/math/c/1/c/c1c0574f6ebb2d780573c350d5c45c5a.png)
</P>
For the decays 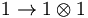 and
and 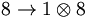 ,
the c.g. coefficients are all 1. Finally, for the decays
,
the c.g. coefficients are all 1. Finally, for the decays 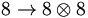 ,
there are 17 c.g. coefficients given as follows
,
there are 17 c.g. coefficients given as follows
 |
 |
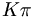 |
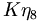 |
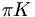 |
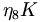 |
|
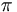 |
 |
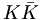 |
 |
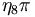 |
 |
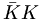 |
 |
 |
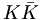 |
 |
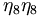 |
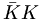 |
|
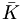 |
 |
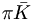 |
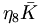 |
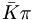 |
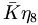 |
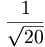 |
 |
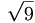 |
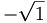 |
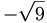 |
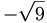 |
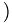 |
|
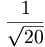 |
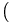 |
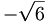 |
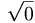 |
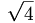 |
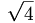 |
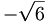 |
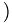 |
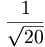 |
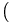 |
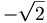 |
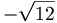 |
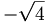 |
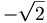 |
 |
|
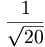 |
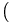 |
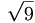 |
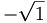 |
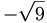 |
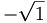 |
 |
Decays of Mesons
We can now use these c.g. coefficients to compute relative decay rates. As an example, let us consider the decay of an 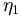 .
.
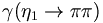 |
 |
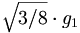 |
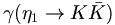 |
 |  |
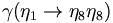 |
 | 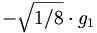 |
This yields the following ratios for the  for the decays of the
for the decays of the
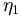 to pairs of pseudoscalar mesons.
to pairs of pseudoscalar mesons.
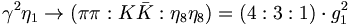
We can also compute the decay to a pair of SU(3) singlets as
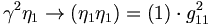
While pure singlet and octet 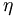 s don't exist, we can use these to expand our calculation to more physical mixing of states. In particular, we will eventually be able to say something about the nonet mixing angles. We consider an f and f' states that are physical mixtures of the octet and singlet states.
s don't exist, we can use these to expand our calculation to more physical mixing of states. In particular, we will eventually be able to say something about the nonet mixing angles. We consider an f and f' states that are physical mixtures of the octet and singlet states.
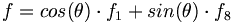
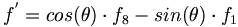
We can now write out several general decays to pairs of pseudoscalar mesons. We first consider the decays of f to pairs of octet mesons.
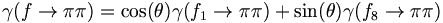
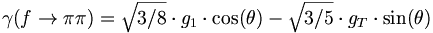 (6)
(6)
Similarly, we can find that
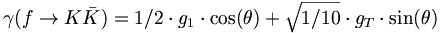 (7)
(7) The same decays can be computed for the f' as well. We now find that
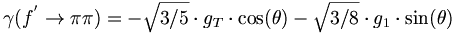 (8)
(8)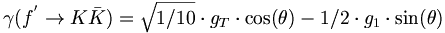 (9)
(9)
The OZI Rule
We could continue in this regard, computing the decays to pairs of 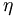 s, but let us stop for a moment, and consider the decay of a pure
s, but let us stop for a moment, and consider the decay of a pure 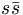 state to a pair of pions.
We can obtain such a state by considering ideal mixing for equations (6) and (7). Recall that for ideal mixing,
state to a pair of pions.
We can obtain such a state by considering ideal mixing for equations (6) and (7). Recall that for ideal mixing, 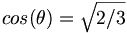 and
and 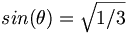 . Thus,
we find that our f' becomes pure
. Thus,
we find that our f' becomes pure 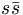 in the limit of ideal mixing. Thus, we can take equation (8) and insert the ideal mixing angle to obtain that
in the limit of ideal mixing. Thus, we can take equation (8) and insert the ideal mixing angle to obtain that
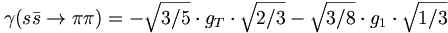
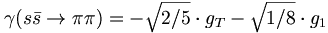 (10)
(10)
If we examine the diagram for such a decay, it must have an 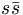 annihilation into some gluonic state which then couples to
annihilation into some gluonic state which then couples to  systems of u and d quarks. Processes that rely on such disconnected diagrams are know to be suppressed, and the so-call OZI rule (for Okubo, Zweig and Iizuka) states that such disconnected diagrams are suppressed. In fact, in the limit of no allowed decays, we can set the rate in equation (10) to be zero. This then yields a relation between g1 and gT.
systems of u and d quarks. Processes that rely on such disconnected diagrams are know to be suppressed, and the so-call OZI rule (for Okubo, Zweig and Iizuka) states that such disconnected diagrams are suppressed. In fact, in the limit of no allowed decays, we can set the rate in equation (10) to be zero. This then yields a relation between g1 and gT.
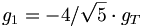 (11)
(11)
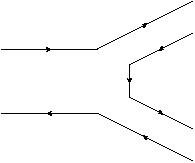
Figure 1: The left figure shows a disconnected quark-line diagram, while the right-hand figure shows a connected quark-line diagram.
We can look for other OZI suppressed decays, and set their rates to zero as well. In this regard, we would[ consider the following two decays.
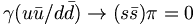 (12)
(12)
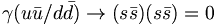 (13)
(13)
As an example of this, we can consider the decay of a  like state, the
like state, the 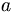 as the
as the 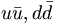 state and compute equation (12).
state and compute equation (12).
![\gamma (a\rightarrow [s{\bar s}]\pi )=-{\sqrt {2/3}}\gamma (a_{{8}}\rightarrow \eta _{{8}}\pi _{{8}})+{\sqrt {1/3}}\gamma (a_{{8}}\rightarrow \eta _{{1}}\pi _{{8}}).](/wiki/images/math/b/1/3/b13d0a459a1f75844a658ac0ee074384.png)
This simplifies to
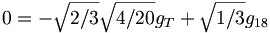
which yields that g18=(2/5)gT. Similarly, we can find that all the decay constants can be expressed in terms of a single constant, gT.
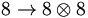 |
gT | gT | (14) |
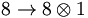 |
g18 | 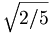 gT gT |
(15) |
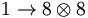 |
g1 | 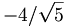 gT gT |
(16) |
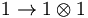 |
g11 | 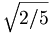 gT gT |
(17) |
The 3P0 Model
Attempts at modeling strong decays date from 1969,
when Micu suggested
that hadron decay proceeds through  pair production with vacuum
quantum numbers,
pair production with vacuum
quantum numbers,  . Since this corresponds to a 3P0
. Since this corresponds to a 3P0
 state, it is now generally referred to as the 3p0
decay model. This suggestion was developed and applied extensively by
Le Yaouanc et al. in the 1970s.
Studies of hadron decays using the 3p0 model
have been
concerned almost exclusively with numerical predictions, and have not led to
any fundamental modifications to the original model.
Recent studies have considered changes in the spatial
dependence of the pair production amplitude as a function of
quark coordinates
but the fundamental decay mechanism is usually not
addressed; this is widely believed to be a nonperturbative process,
involving ``flux tube breaking".
There have been some studies of the decay
mechanism which consider an alternative phenomenological
model in which the
state, it is now generally referred to as the 3p0
decay model. This suggestion was developed and applied extensively by
Le Yaouanc et al. in the 1970s.
Studies of hadron decays using the 3p0 model
have been
concerned almost exclusively with numerical predictions, and have not led to
any fundamental modifications to the original model.
Recent studies have considered changes in the spatial
dependence of the pair production amplitude as a function of
quark coordinates
but the fundamental decay mechanism is usually not
addressed; this is widely believed to be a nonperturbative process,
involving ``flux tube breaking".
There have been some studies of the decay
mechanism which consider an alternative phenomenological
model in which the  pair is produced with 3S1
quantum numbers; this possibility however appears to
disagree with experiment.
pair is produced with 3S1
quantum numbers; this possibility however appears to
disagree with experiment.
References
Meson Decay References
- Higher quarkonia, T.Barnes, F.E. Close, P.R. Page and E.S. Swanson, Phys. Rev. D55 (1997), 4157-4188 PRD.
- On the mechanism of open flavor strong decays, E.S. Ackleh, T. Barnes and E.S. Swanson, Phys. Rev. D54 (1996), 6811-6829, PRD.
- Hybrid and conventional mesons in the flux tube model: Numerical studies and their phenomenological implications, T. Barnes, F.E. Close and E.S. Swanson, Phys. Rev. D52 (1995), 5242-5256, PRD.
- The Quenched Approximation In The Quark Model, P. Geiger and N. Isgur, Phys. Rev. D41 (1990), 1595, PRD.
- Meson Decays by Flux Tube Breaking, R. Kokoski and N. Isgur, Phys. Rev. D35 (1987), 907, PRD.
- A Flux Tube Model for Hadrons in QCD, N. Isgur, J. E. Paton, Phys. Rev. D31 (1985), 2910, PRD.
- A Flux Tube Model for Hadrons N. Isgur and J. E. Paton, Phys. Lett. B124, (1983), 247, Science Direct.
Hybrid Meson Decay References
- The "forbidden" decays of hybrid mesons to π ρ can be large, F.E. Close and J.J. Dudek, Phys. Rev. D70 (2004), 094015, arXiv.
- Hybrid Meson Decay Phenomenology, P.R. Page, E.S. Swanson and A.P. Szczepaniak, Phys. Rev. D59 (1999), 034016, arXiv.
- Why Hybrid Meson Coupling to Two S-wave Mesons is Suppressed, P.R. Page, Phys. Lett. B402 (1996), 183-188, arXiv.
- Q anti-Q G Hermaphrodite Mesons in the MIT Bag Model, T. Barnes, F.E. Close, F. de Viron and J. Weyers, Nucl. Phys. B224 (1983), 241, Science Direct.
- Gluonic Excitations of Mesons: Why They Are Missing and Where to Find Them, N. Isgur, R. Kokoski and J. E. Paton, Phys. Rev. Lett. 54 (1985), 869, PRL.